Gossip 协议总结

Gossip 协议是一种弱最终一致性算法，主要用于解决大规模去中心化 P2P 网络中的数据一致性问题，其显著特点在于简单易于理解，并且不要求节点间均可以相互通信，只要一个节点能与部分节点通信，那它就可以把数据变更消息广播至整个联通网络中。

Gossip 协议最有名的应用包括 Redis-Cluster，Bitcoin，Cassandra 等。

历史

Gossip 协议最早发布于 1989 年的 ACM 会议论文 Epidemic Algorithms for Replicated Database Maintenance 中，论文中是用来解决分布式数据库多副本一致性问题的，这是一个最终一致性算法。

由于此算法仅能保证最终一致性而非强一致性，而且达到一致的时间不可控，因此目前更多的是被用于各种 P2P 应用中。

设计哲学

如同其名字一样，消息的传播就像谣言的传播一样，一传十，十传百，百传千千万。

基本原理

若一个节点需要向其他节点广播发送消息，则：

1. 随机选择 N 个尚未发送过消息的邻接节点发送消息；
2. 等待一段时间，再重复上述步骤；

当一个节点收到其他节点的广播消息时，更新自己的数据，并向除源节点外其他节点广播数据。

网络上诸多文章对 Gossip 协议的介绍基本就到此为止了，基本还会配上这样一张传播示意图：

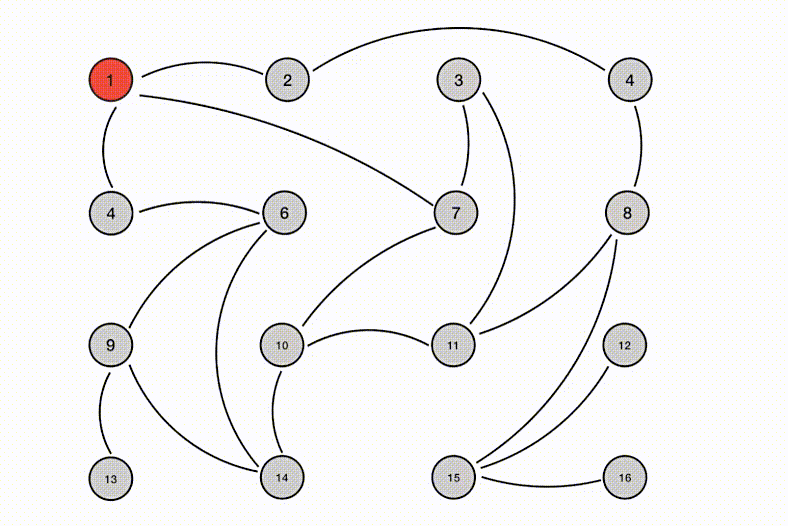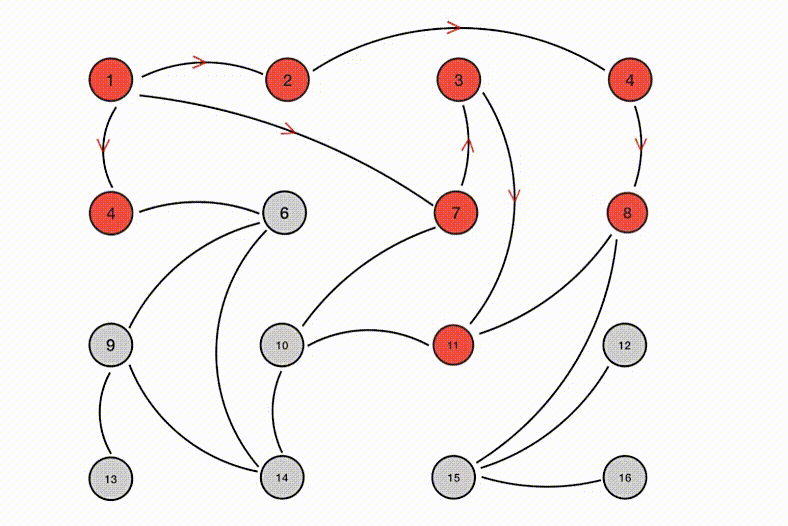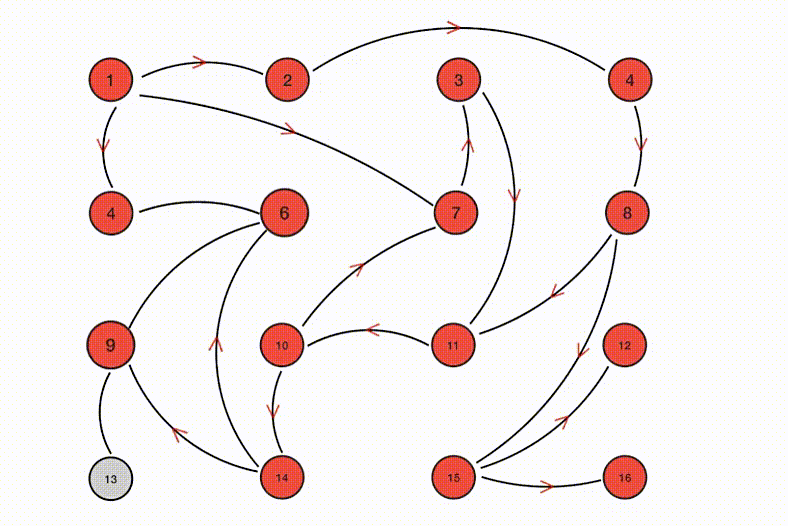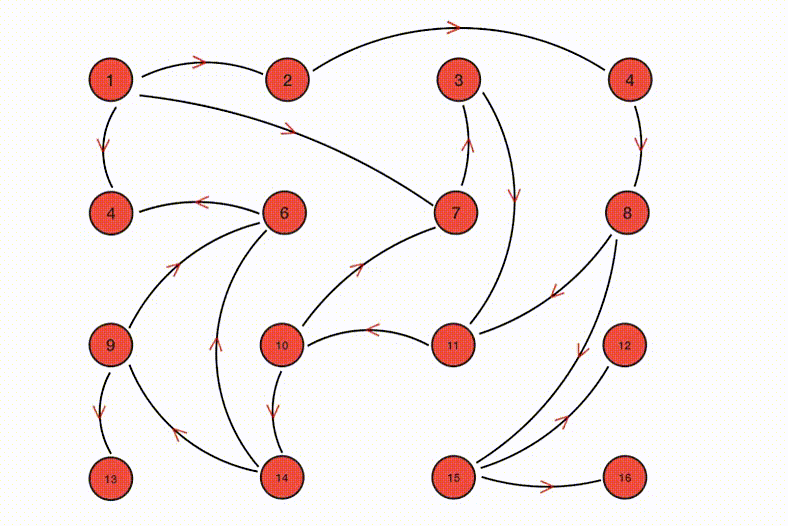
然而根据上述如此抽象的描述可以说是没法搭建出实际有用的系统来的。粗略想想就会发现几个核心问题没有被解决：

• 收到消息后该如何更新？直接无脑覆盖已有数据？那如果集群中有两个节点都在更新相同内容怎么处理？此时如何保证集群能达到最终一致性，而不会发生振荡？
• 上述广播的过程是一直循环进行的还是发送完一轮就会停止？

其实在 Gossip 的原始论文中对这些问题是有更细致的讨论和处理的，Márk Jelasity 在 Self-organising software. From natural to artificial adaptation 一书中也有详细论述，二者基本是一致的。

详细实现方法

消息或数据的抽象

实际的消息或数据的形式是由具体应用决定的，不过不妨将其抽象为 K-V-T 集合，即若干条 Key -> Value + Time，这里的 Time 可以是实际的时间戳，也可以是其他类似 Version 的值。

更新数据时并不会直接无脑的去覆盖数据，而是会比较 Time：

Update(k, v, t) {
  if (this.t < t) {
    this.k.v = v;
  }
}

Gossip 的论文中就是使用了时间戳来作为这个 Time，不过这感觉会存在一个问题：

如何保证全局时间戳的一致性呢？如果无法保证，那会不会造成节点间的不平等？即时间较晚那个节点相当于就被赋予了更高的优先级？

算法基本策略

Gossip 算法有三种基本策略：

• Direct mail，直接邮寄
• Anti-entropy，反熵传播
• Rumor mongering (Complex Epidemics)，谣言传播（复杂传染）

在后两种策略中，消息的交互通信模式又可以分为三种：

• Push
• Pull
• Push/Pull

在下文描述中，使用 S 表示某一节点的邻接节点集合。

Direct mail

当某一节点有数据发生更新时，触发通知其他所有节点的流程：

for(s : S) {
  s.Send(k, v, t);
}

收到数据的节点更新自己的数据，若成功更新继续重复上述流程通知自己的邻接节点。

此策略由于只发送一次数据，所以并不一定可靠。

Anti-entropy

此策略在 Márk Jelasity 的书中被称为 SI 模型，其工作流程是每个节点均周期性的选择部分邻接节点同步更新数据：

while(true) {
  for (s : RandomChoice(S)) {
    s.ResolveDifference(k, v, t);
  }
  delay(...);
}

三种消息交互模式的区别就在于 ResolveDifference 的实现方式不同：

• Push 模式下节点 A 将 K-V-T 数据发送给节点 B，节点 B 更新自己的数据；
• Pull 模式下节点 A 发起请求，将自己已有的 K-T 数据发给节点 B，节点 B 收到后与自己的数据进行比较，将更新或节点 A 没有的 K-V-T 数据发送给节点 A，节点 A 更新自己的数据；
• Push/Pull 模式即为上述两种模式的结合，节点 A 推送 K-V-T 至节点 B，节点 B 更新完后把需要节点 A 更新的 K-V-T 再推送回节点 A，节点 A 再更新自己的数据。

上述描述中 Push/Pull 模式的流程与大部分文章中写的有所区别，在大部分文章中，Push/Pull 模式就是简单的 Pull + Push，此时会存在 3 次网络交互，此处进行了一些优化，如果先做 Push 再做 Pull 则可以减少一次网络交互。

在 Direct mail 形式下使用的就是 Push 通信模式，因此 Direct mail 策略可以视为是只执行一次的使用 Push 模式的 Anti-entropy 策略；

一般而言，显然是 Push/Pull 模式收敛得最快。

此方法中，发送的 K-V-T 根据论文的描述应该是数据全集，这就导致需要交互的数据量极大，甚至是完全不可行的。而且这个交互过程是一直都在进行永不停止的，这也会造成较大的带宽浪费。

Rumor mongering (Complex Epidemics)

针对 Anti-entropy 策略做了些改进，每个节点加入一个状态，可能取值有：

• S: Susceptible, 不存在数据更新
• I: Infective, 存在数据更新且需要广播
• R: Removed, 存在数据更新，然而不广播

故此策略在 Márk Jelasity 的书中被称为 SIR 模型。

其中 S 状态是节点的初始值，仅当没有数据更新时才会处于此状态中，一旦发生了数据更新就永远也不可能回到此状态中。因此感觉此状态是为了理论的完美性才引入的，从实际实现的角度来看完全可以忽略此状态。

此外还需要再引入一条 Feedback 消息，当某个节点 B 收到节点 A 发来的 Push 消息后会回复节点 A 此消息。

此时状态迁移就会变得很简单，一旦发生数据更新（通过与其他节点交互或系统其他部分修改数据）就会成为 I 状态；一旦收到 Feedback 消息，则有一定概率会变成 R 状态；

当节点处于 I 状态时，行为与 Anti-entropy 策略相同；当节点处于 R 状态时，不进行周期性的节点同步更新。此策略的目的正是通过引入 R 状态来让节点间的交互可以在一段时间内停止。

上述变成 R 状态的一定概率在论文中用 $1/k$ 表示，此概率是怎么确定的呢？学术点的做法是根据集群规模理论计算出来，当然实际使用的时候一般都是试出来的，此概率越高则系统收敛速度越快，然而也越容易无法保证最终一致性。

进一步优化与工程实践

论文的内容就到此为止了，然而仔细揣摩下上述策略，其实有一些点是可以进一步优化的。

首先在消息的设计上，由于 Push/Pull 模式是最为完善的，可以均选用此策略，此时消息就可以简化为 PushReq & PullRes 两条。

Rumor mongering 策略中引入的 Feedback 消息在此设计下其实是多余的，一旦收到 PullRes 即等同于收到了 Feedback 消息。

另一个可能的优化点在于，PushReq 中携带的 K-V-T 是否可能不是全量数据，只发送增量数据，这么做需要思考以下一些难点：

• 需要在 PushReq 中加入特殊的字段表明此请求是增量单向 Push，PullRes 中不需要回复缺失 K-V-T。然而加入此字段后会不会让整个系统只有 Push 而没有 Pull 的能力呢？还是除了初始化时其他时候不需要 Pull 也可以正常工作呢？
• 如何记录哪些 K-V 是变化了的呢？一个想法是是否可以利用时间信息，比较上一次同步的时间与数据中的时间戳 T
• 在数据会持续更新的情况下，会不会由于节点被错误的置为 R 状态而导致数据不一致？

新节点加入时，只需要发送空的 PushReq 即可，此时相当于 Pull 模式去主动拉数据。

适用场景及优缺点

Gossip 协议的适用场景相对比较确定：

1. 集群没有中心节点，且各节点的地位是平等的；
2. 集群拓扑结构是网状结构，且单个节点只能与部分邻接节点通信，不能与全部节点通信；
3. 系统不要求强一致性，甚至最终一致性都不要求，只要求大部分节点能达到最终一致即可；

第 2 点是 Gossip 协议最显著的优点，在这样的去中心化拓扑结构下，其他很多一致性算法都是没法正常工作的，因此在 P2P 网络中 Gossip 协议取得了广泛的应用；而第 3 点则是 Gossip 协议最大的局限性，即它不是强一致性协议。

如果系统具有特性 1 & 2 而又要求强一致能否实现呢？好像还没有听过这样的算法……感觉可以搞个 Paxos + Gossip 的混合算法出来？这估计是个蛮有意思的东西吧……

Gossip 协议还有哪些显著优点呢：

• 足够简单易于理解及实现；
• 扩展性及容错性极好，节点的加入和删除可以很平滑的处理；
• 对于大规模网络来说，传播速度足够快，且对集群规模的扩大不敏感，准确一点来说，消息传播所需次数是 $\log(N)$ 级别的。

至于它的缺点，主要就是前文所述的，它不是强一致协议，甚至都不能保证最终一致性。

参考资料

P2P 网络核心技术：Gossip 协议
Gossip 协议详解
一万字详解 Redis Cluster Gossip 协议
分布式系列 Gossip协议