Population Count算法

所谓Population Count算法，即是指计算一个二进制数中1的个数的算法。具体来说，就是任意给定一个无符号整数N，求N的二进制表示中1的个数，比如N = 5（0101）时，返回2；N = 15（1111）时，返回4。

这个问题是一个经典的面试题目，在实际中也有应用。关于这个问题，以下两篇博客文章中有较详细的论述：

详解二进制数中1的个数
算法-求二进制数中1的个数

在此，仅对其中一些较为常规和较为巧妙的方法做一总结，并比较一下他们的执行效率。

直接法1

直接逐位判断，最直接也是最低效的方法。

char CountOne1(unsigned int num)
{
  char N = 8 * sizeof(num);
  char Count = 0;
  while (N--)
  {
    Count += num & 1;
    num >>= 1;
  }
  return Count;
}

直接法2

在“直接法1”的基础上进行改进，当移位结果为0后就退出循环，这样循环次数与首位1的位置有关。最优情况下只循环一次，最坏情况下循环N次。

char CountOne2(unsigned int num)
{
  char Count;
  for (Count = 0; num != 0; num >>= 1)
  {
    Count += num & 1;
  }
  return Count;
}

逐次清除最低位1

此方法利用num &= (num - 1)可清除最低位1的原理进行计数。
num与num - 1的区别在于，num的最低位1在num - 1中变为了0，故二者取与后即可清除最低位1.

int CountOne3(unsigned int num)
{
  char Count;
  for (Count = 0; num != 0; Count++)
  {
      num &= (num - 1);
  }
  return Count;
}

分支法

思路类似二分法，两两相加后即可得到结果，见下图：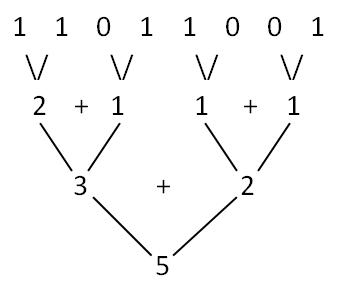

在详解二进制数中1的个数中对此有详细描述。此方法复杂度为Log(N)(之前几种方法复杂度均为N)，对于32位整数只需要计算5次即可。

char CountOne4(unsigned int num) 
{ 
  num = (num & 0x55555555) + ((num >> 1)  & 0x55555555); 
  num = (num & 0x33333333) + ((num >> 2)  & 0x33333333); 
  num = (num & 0x0f0f0f0f) + ((num >> 4)  & 0x0f0f0f0f); 
  num = (num & 0x00ff00ff) + ((num >> 8)  & 0x00ff00ff); 
  num = (num & 0x0000ffff) + ((num >> 16) & 0x0000ffff); 

  return num ; 
}

三分法

这是一种很巧妙的方法，在此对其原理不多做说明，可参考之前提到的那两篇博客文章。

char CountOne5(unsigned int num)
{
  unsigned int tmp = num - ((num >> 1) & 033333333333) - ((num >> 2) & 011111111111);
  return ( (tmp + (tmp >> 3) ) & 030707070707) % 63;
}

CPU指令实现

部分CPU中直接提供了指令来完成这一操作，这无疑是效率最高且最为简洁的方法。

在Intel x86中，如果CPU支持SSE4指令集，那可以使用POPCNT指令来计算二进制数中1的个数，实验表明，这应该是一个单周期指令，所以这无疑是最优的解决方案。

在MSVC下，可通过_mm_popcnt_u32()函数来调用POPCNT指令，详细信息可参考MSDN上的帮助。
调用示例如下:

#include <nmmintrin.h>

Count = _mm_popcnt_u32(num);

在GCC下，可直接调用__builtin_popcountll()函数，编译时加上编译选项-mpopcnt即可，此时编译器会自动使用POPCNT指令。

在ARM中，也有类似的指令，比如POPCOUNT宏（需要约10个时钟周期），NEON SIMD指令集中的VCNT及CNT指令。

POPCNT指令应该是有其实际重要作用的，比如在OpenCV的编译过程中就可以选择是否启用POPCNT指令。

执行时间对比

毫无疑问，直接调用CPU指令是最佳的解决方案，将其执行时间规定为1，对其他算法的执行时间进行归一化处理，结果如下：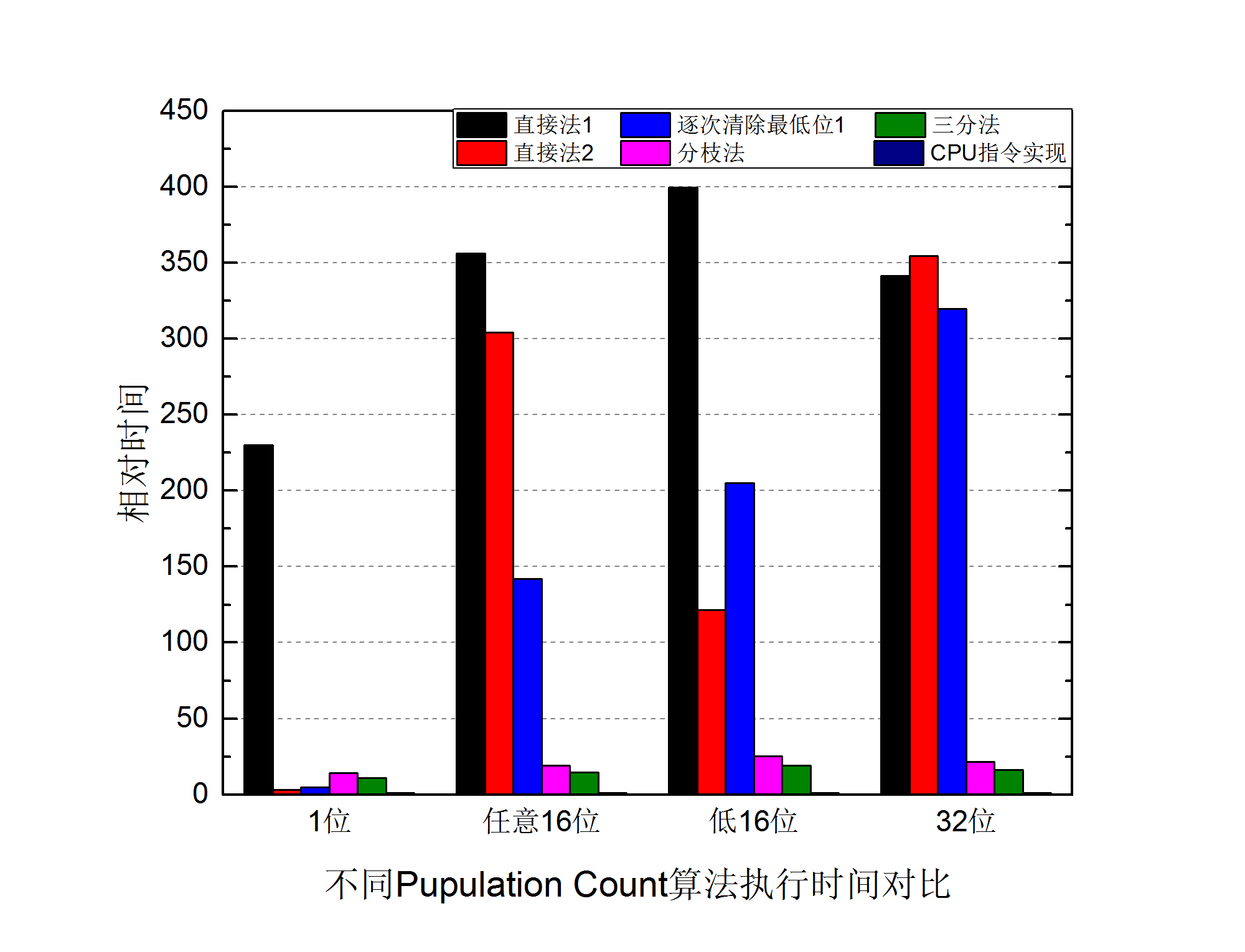

从中可以看到，除了特别简单的情况下（如0x01），分枝法与三分法的执行效率是最好的，且这两种算法是稳定的算法，其执行时间不依赖于输入数据。逐次清除最低位1法在1的个数较少时也不失为一种好方法。