LeetCode 142. Linked List Cycle II (Medium)

给定一个链表，返回链表中环的开始节点，若没有环，返回null。

原始问题

https://leetcode.com/problems/linked-list-cycle-ii/

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Note: Do not modify the linked list.

Follow up:
Can you solve it without using extra space?

解题思路

类似LeetCode 141的解法，只是之后还要求出环开始的节点，这依赖于一些数学关系，下面来简要推导一下。

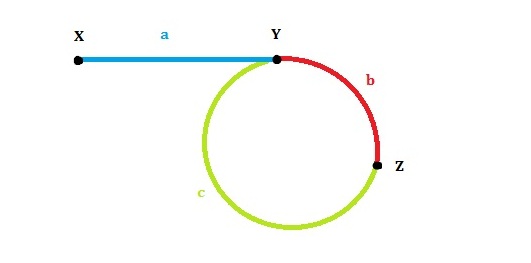
如图所示，假设slow指针运动到$Y$节点时，fast指针位于环中任意位置（图中未标出），其距$Y$点的距离为$m$。首先证明当slow指针与fast指针相遇于环中某一点$Z$时，slow指针移动距离$b$小于环的长度$L$，且fast指针只会比slow指针多移动一圈。

假设此时slow指针移动距离为$b$($b$ < $L$)，fast指针比slow指针多移动了$N$圈，则：
$$b=m+2b-NL$$
$$\Rightarrow b=NL-m$$
$$\because 0 \leqslant b \leqslant L, 0 \leqslant m \leqslant L$$
$$\therefore N = 1$$
$$\Rightarrow b=L-m$$
对任意$m$及$L$，均可由上式确定唯一的$b$，故原命题成立。

下面在此基础上推导$a$与$c$之间的关系，应用上面得出的结论，两指针相遇时有：

$$2(a+b)=a+b+KL$$
式中$K$表示相遇时fast指针在环中运行的圈数。
$$\Rightarrow a=KL-b$$
$$\Rightarrow a=(K-1)L+L-b$$
$$\Rightarrow a=(K-1)L+c$$

上式意味着，若slow与fast指针相遇于$Z$点后，slow指针继续前进，同时增加一个指针p从$X$点出发，则slow与p的相遇点必定是$Y$，这也就是需要返回的节点。根据上述思路即可写出代码。

AC代码

C语言

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * slow, * fast, * p;
    
    if (head == NULL) {
        return NULL;
    }
    
    slow = head;
    fast = head;
    p = head;
    
    while (fast->next != NULL && fast->next->next != NULL) {
        slow = slow->next;
        fast = fast->next->next;
        
        if (slow == fast) {
            while (p != slow) {
                p = p->next;
                slow = slow->next;
            }
            return p;
        }
    }
    
    return NULL;
}

相关题目

LeetCode 141. Linked List Cycle (Easy)
LeetCode 160. Intersection of Two Linked Lists (Easy)